Machine learning algorithms can be used for market prediction with Zorro's advise functions. Due to the low signal-to-noise ratio and to ever-changing market conditions of price series, analyzing the market is an ambitious task for machine learning. But since the price curves are not completely random, even relatively simple machine learning methods, such as in the DeepLearn script, can predict the next price movement with a better than 50% success rate. If the success rate is high enough to overcome transactions costs - at or above 55% accuracy - we can expect a steadily rising profit curve.
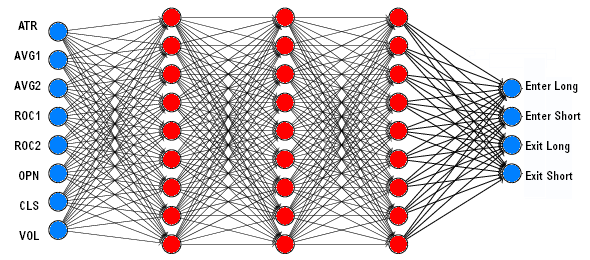
Compared with other machine learning algorithms, such as Random Forests or Support Vector Machines, deep learning systems combine a high success rate with litle programming effort. A linear neural network with 8 inputs driven by indicators and 4 outputs for buying and selling has a structure like this:
Deep learning uses linear or special neural network structures (convolution layers, LSTM) with a large number of neurons and hidden layers. Some parameters common for most neural networks:
Here's a short description of installation and usage of 5 popular R or Python based deep learning packages: Deepnet, Torch, Keras/Tensorflow, H2O, and MxNet. Each comes with an short example of a (not really deep) linear neural net with one hidden layer.
library('deepnet')
neural.train = function(model,XY)
{
XY <- as.matrix(XY)
X <- XY[,-ncol(XY)]
Y <- XY[,ncol(XY)]
Y <- ifelse(Y > 0,1,0)
Models[[model]] <<- sae.dnn.train(X,Y,
hidden = c(30),
learningrate = 0.5,
momentum = 0.5,
learningrate_scale = 1.0,
output = "sigm",
sae_output = "linear",
numepochs = 100,
batchsize = 100)
}
neural.predict = function(model,X)
{
if(is.vector(X)) X <- t(X)
return(nn.predict(Models[[model]],X))
}
neural.save = function(name)
{
save(Models,file=name)
}
neural.init = function()
{
set.seed(365)
Models <<- vector("list")
}
You need to write a .cpp script and run it with the 64-bit Zorro version. Include pynet.cpp, which contains the neural function for Python. Then write the PyTorch script, with the same name as your strategy, but extension .py. Example:
import torch
from torch import nn
import math
import numpy as np
Path = "Data/Signals.csv"
Device = "cpu"
NumSignals = 8
Batch = 15
Split = 90
Epochs = 30
Neurons = 256
Rate = 0.001
Models = []
def neural_init():
global Device
Device = (
"cuda"
if torch.cuda.is_available()
else "mps"
if torch.backends.mps.is_available()
else "cpu"
)
def network():
model = nn.Sequential(
nn.Linear(NumSignals,Neurons),
nn.ReLU(),
nn.Linear(Neurons,Neurons),
nn.ReLU(),
nn.Linear(Neurons,1),
nn.Sigmoid()
).to(Device)
loss = nn.BCELoss()
optimizer = torch.optim.Adam(model.parameters(),lr=Rate)
return model,loss,optimizer
def data(Path):
global NumSignals
Xy = np.loadtxt(Path,delimiter=',')
NumSignals = len(Xy[0,:])-1
return Xy
def split(Xy):
X = torch.tensor(Xy[:,0:NumSignals],dtype=torch.float32,device=Device)
y = torch.tensor(Xy[:,NumSignals].reshape(-1,1),dtype=torch.float32,device=Device)
y = torch.where(y > 0.,1.,0.)
return X,y
def train(N,Xy):
global Models
model,loss,optimizer = network()
X,y = split(Xy)
for j in range(Epochs):
for i in range(0,len(X),Batch):
y_pred = model(X[i:i+Batch])
Loss = loss(y_pred,y[i:i+Batch])
optimizer.zero_grad()
Loss.backward()
optimizer.step()
print(f"Epoch {j}, Loss {Loss.item():>5f}")
Models.append(model)
return Loss.item()*100
def neural_train(N,Path):
Xy = data(Path)
return train(N,Xy)
def neural_predict(N,X):
if N >= len(Models):
print(f"Error: Predict {N} >= {len(Models)}")
return 0
model = Models[N]
X = torch.tensor(X,dtype=torch.float32,device=Device)
with torch.no_grad():
y_pred = model(X)
return y_pred
def neural_save(Path):
global Models
torch.save(Models,Path)
print(f"{len(Models)} models saved")
def neural_load(Path):
global Models
Models.clear()
Models = torch.load(Path)
for i in range(len(Models)):
Models[i].eval()
print(f"{len(Models)} models loaded")
Installing the GPU version is more complex, since Tensorflow supports Windows only in CPU mode. So you need to either run Zorro on Linux, or run Keras and Tensorflow under WSL for GPU-based training. Multiple cores are only available on a CPU, not on a GPU.
Example to use Keras in your strategy:
library('keras')
neural.train = function(model,XY)
{
X <- data.matrix(XY[,-ncol(XY)])
Y <- XY[,ncol(XY)]
Y <- ifelse(Y > 0,1,0)
Model <- keras_model_sequential()
Model %>%
layer_dense(units=30,activation='relu',input_shape = c(ncol(X))) %>%
layer_dropout(rate = 0.2) %>%
layer_dense(units = 1, activation = 'sigmoid')
Model %>% compile(
loss = 'binary_crossentropy',
optimizer = optimizer_rmsprop(),
metrics = c('accuracy'))
Model %>% fit(X, Y,
epochs = 20, batch_size = 20,
validation_split = 0, shuffle = FALSE)
Models[[model]] <<- Model
}
neural.predict = function(model,X)
{
if(is.vector(X)) X <- t(X)
X <- as.matrix(X)
Y <- Models[[model]] %>% predict_proba(X)
return(ifelse(Y > 0.5,1,0))
}
neural.save = function(name)
{
for(i in c(1:length(Models)))
Models[[i]] <<- serialize_model(Models[[i]])
save(Models,file=name)
}
neural.load = function(name)
{
load(name,.GlobalEnv)
for(i in c(1:length(Models)))
Models[[i]] <<- unserialize_model(Models[[i]])
}
neural.init = function()
{
set.seed(365)
Models <<- vector("list")
}
cran <- getOption("repos")
cran["dmlc"] <- "https://s3-us-west-2.amazonaws.com/apache-mxnet/R/CRAN/"
options(repos = cran)
install.packages('mxnet')
The MxNet R script:library('mxnet')
neural.train = function(model,XY)
{
X <- data.matrix(XY[,-ncol(XY)])
Y <- XY[,ncol(XY)]
Y <- ifelse(Y > 0,1,0)
Models[[model]] <<- mx.mlp(X,Y,
hidden_node = c(30),
out_node = 2,
activation = "sigmoid",
out_activation = "softmax",
num.round = 20,
array.batch.size = 20,
learning.rate = 0.05,
momentum = 0.9,
eval.metric = mx.metric.accuracy)
}
neural.predict = function(model,X)
{
if(is.vector(X)) X <- t(X)
X <- data.matrix(X)
Y <- predict(Models[[model]],X)
return(ifelse(Y[1,] > Y[2,],0,1))
}
neural.save = function(name)
{
save(Models,file=name)
}
neural.init = function()
{
mx.set.seed(365)
Models <<- vector("list")
}